

| Home | Order | Lost piece? | ||
| History | Hints | Web friends | ||
| References | Solutions | Challenges! | ||
 The Gnomon of the Zhou, by Liu Hui (around 263 AD) can be considered as the first general geometric proof by dissection of the Pythagoras' theorem. Thabit Ibn Qurra' (826 - 901) and Bhaskara Acharya (1114 - 1185), both provide very famous geometric proofs by dissection. If we could ask to any of them how to cut a square in three squares of identical areas, they would probably reply: “Use my dissection to divide the square into two squares of 1/3 and 2/3 of its surface, then simply cut the square of surface 2/3 in two!”. These proofs of the Pythagoras' theorem by dissection give valid solutions but aren't minimal. 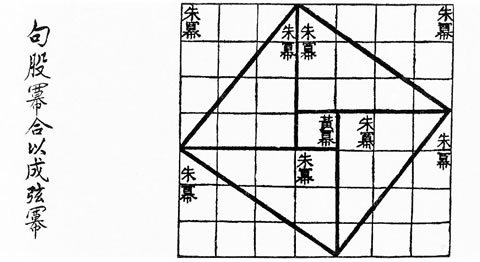
Zhou Bi Suan Jing Gnomon (Liu Hui vers 263 AD) From the 8th century AD up to the 15th century, Muslims dominated the world through their science (see Encyclopedia of the History of Arabic Science Roshdi Rashed (1996), Vol. 2 Chap. 14, by B.A. Rosenfeld and A.P. Youschkevitch). The craftsmen who built the mosques used mosaics adorned with geometric patterns of great aesthetic value and sometimes found themselves faced with the complex problem of dissections. One such problem was figuring out how to assemble three identical squares to form a new one, using a minimal number of pieces. Muhammad ibn Muhammad ibn Yahya ibn Isma'il ibn al-'Abbas Abu'l-Wafa' Al-Buzajani (940 - 998), born in Iran, was the most skillful and knowledgeable professional geometry expert of his time. In his treatise Kitab fima ya htaju ilayhi al-sani' min a'mal al-handasa (On the Geometric Constructions Necessary for the Artisan, chapter on dividing and assembling squares), Abu'l-Wafa' gave the first correct nine-piece solution to this problem. One of the copies of his treatise can be seen at the "Bibliothèque nationale française de Paris". In this treatise, he wrote: “I was present at a meeting in which a number of geometers and artisans participated. They were asked about the construction of a square from three squares. Geometers easily constructed a line such that the square of it is equal to the three squares but none of the artisans was satisfied. They wanted to divide those squares into pieces from which one square can be assembled. [...] Some of the artisans located one of these squares in the middle and divided the next one on its diagonal and divided the third square into one isosceles right triangle and two congruent trapezoids and assembled together.” 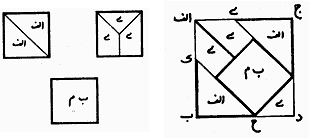 A wrong solution! (credit Reza Sarhangi) If we assume that the small central square has unit length, then the diagonal of the big square must be 1 + square_root(2) which is less than square_root(6), the diagonal of a square of area 3. Thus this construction is wrong. Abu'l-Wafa' has generalized his dissection for proving the Pythagorean theorem (see Alpay Özdural in references). A representation of his generalization can be seen in many mosaics on the largest mosque in Iran, the Jameh Mosque of Isfahan (figure below). 
Jameh Mosque of Isfahan Around 1300, a nine-piece solution and an eight-piece solution were found, presumably by Abu Bakr al-Khalil al-Tajir al-Rasadi. It was not until the 18th and 19th centuries that mathematicians such as Jean-Étienne Montucla, Jacques Ozanam, Philip Kelland, Paul Busschop, Le Colonel De Coatpont and Edouard Lucas revisited this issue. Henry Perigal found the first solution which uses only six-pieces, around the 1830s - 1840s (according to a note in appendix after Rogers' 1897 publication), but published his technique only in 1875, and the solution itself in 1891. His solution is similar to one of the two proposed by Abu Bakrs al-Khalil. The Perigal version is asymmetric but, by shifting the diagonal of the cut, has two fewer pieces. It is noteworthy to mention that Philipe Kelland published a very similar technique for dissecting a gnomon (L-shaped part of a square with one corner missing) in 1855. Henry Perigal also rediscovered the Abu'l-wafa' dissection for proving Pythagora's theorem. He considered this proof to be his best work and later made an engraving of this dissection for his tomb. 

Henry Perigal's grave During the 20th century, H.E. Dudeney and Sam Loyd's both republished Perigal's six-piece solution. New solutions attempts were published in a few mathematics journals, using more than six pieces. In the 21st century, Greg N. Frederickson found a seven-piece hinge-able and symmetric solution, and Nobuyuki Yoshigahara found a nine-piece dissection using exactly three times three identical pieces (which is indeed a seven-piece solution). In 2010, Christian Blanvillain and János Pach provide a six-piece symetric family of solutions using non-convex pieces. Greg N. Frederickson remarks that for one particular position, all the six pieces have exactly the same area! which makes this dissection really unique. The Quadratum Cubicum is composed with nine of those solutions, selected for their aesthetic and their historical importance. For more information on the fabulous history of this problem, and on dissections in general, we refer the reader to the bibliography's links and the three excellent books by Prof. Greg N. Frederickson, that will present to you the puzzle solutions throughout the ages and much more! |
||
| Home | Order | Lost piece? | ||
| History | Hints | Web friends | ||
| References | Solutions | Challenges! | ||